
図形だけで描く簡単な模様の描き方をこれまで2回にわたって紹介しました。
1回目は、単純な図形をただ並べるだけの模様。
2回目は、その単純な模様をアレンジする方法です。
そして今回は、そのアレンジをさらに展開させて描く方法、アレンジの組み合わせについてをお伝えします。
図形だけで描く模様とは?簡単なおさらい。
まずは前回までのおさらいです。
▼基本の模様(羅列模様)
単純な図形で作る模様として、同じ形と大きさの図形をただ並べるだけの描き方があります。
図形は「菱形」「三角形」「クの字図形」を使いました。

これをひたすら並べていくと…

このように、図形を並べるだけでも十分模様にはなります。
でも単調に感じるので、これにアレンジを加えた模様のバリエーションがこちらです。
▼菱形のアレンジ

▼三角形のアレンジ

▼クの字図形のアレンジ

このように、それぞれ一例ずつですが
アレンジ方法は大きく4つに分けることができます。
ズラす(並行移動)
サイズを変える
重ねる
向きを変える
そしてこのアレンジを2つ以上組み合わせれば、さらに色んな模様が生み出せるということです!
ただしこれは、20年以上模様を描き続けて独学で得た私なりの模様の描き方・作り方です。
世界共通の模様の法則とは少しニュアンスが違う部分もありますので、あくまで参考程度にご覧ください。
※世界共通の模様の法則についてもいずれ当ブログで紹介する予定です。
アレンジの組み合わせとは?
それでは早速、模様の例を出しながら説明していきます。
これまで同様、グリッドノート(方眼ノート)で描く前提での内容となります。
お手元にご用意いただければと思います。
見やすいサンプルにするため、画像は全てIllustratorで作成しています。画像のようにまっすぐな線を引くには定規の使用をオススメします。画像の例は参考までにご覧ください。
まずは次の模様をご覧ください。
菱形の羅列模様をアレンジしたものです。
2つのアレンジ方法を組み合わせて描きました。

どのアレンジを組み合わせているか、見えてくるでしょうか。
小さい菱形があるので一見 ”サイズを変える”だけにも見えますが、菱形同士が重なってもいますよね。
ということでこれは『サイズを変える』と 『重ねる』2つのアレンジを組み合わせています。
さらにもう一つのアレンジ『ズラす(並行移動)』を付け加えると…

こうなります!縦一列ずつ、3マスずらして配置しています。
さらに『向きを変える』を加えると…

だいぶ印象が変わりましたが、小さい菱形の向きを変えました。
菱形を横に90度倒すと正方形になる、ということを利用して小さい方の菱形をマス目に沿って正方形に描いただけです。
もとの菱形と正方形では若干大きさが異なりますが、グリッドの目盛りに沿って線を描くと自然と変わってしまうので、あまり気にしないでも大丈夫です。
という具合に、どれも単純な幾何学模様ですが、アレンジ方法を一つに絞るより2つ以上組み合わせることによって色々なバリエーションの模様を描くことが可能となるのです。
具体的な例と一緒に描いてみよう
では、こんな感じでアレンジ組み合わせの例をいくつか出していこうと思います。
考えれば考えるほど色んなパターンが作れますが、多くなってキリがないのでまずはわかりやすい模様を紹介します。
ぜひ真似して描いてみてください。
サイズを変える × 重ねる
始めに、2つのアレンジの組み合わせです。
個人的に一番簡単で変化がわかりやすいと感じるのが『サイズを変える』『重ねる』の組み合わせです。
菱形を使っていくつか例をご紹介します。
例1
縦の列ごとに図形のサイズを変えてそれを繰り返し重ねると、このような模様が出来上がります。
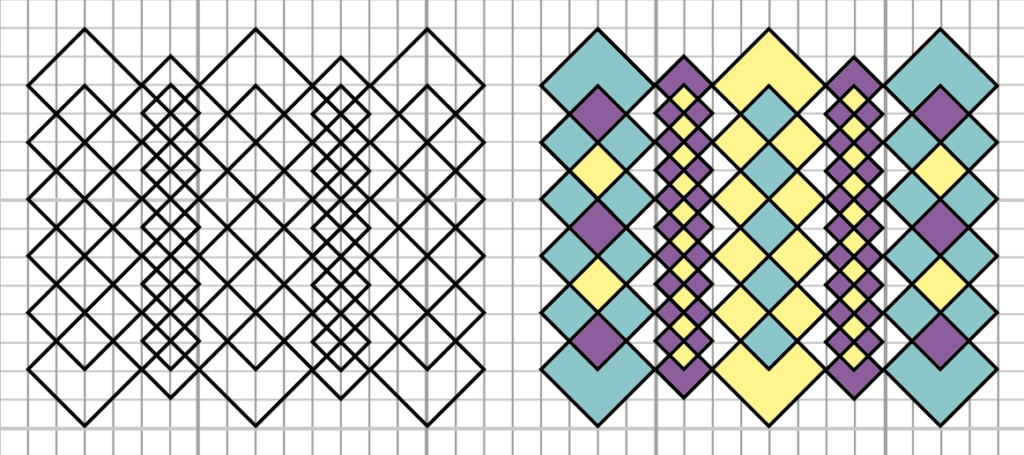
例2
例1の模様を縦横サイズを変えるのもありですね。

例3
小さい菱形をもっとわかりやすく、シンプルに重ねます。
すごく単純な模様になりましたが、これも一つのアレンジ方法です。

例4
小さいサイズの菱形の数を増やして、大きい菱形にキレイに重ねてみましょう。

サイズを変える × 重ねる × ズラす (並行移動)
では、ここまでの例に”ズラす(移動)”のアレンジを加えてみます。
マス目をよく見ながら、一マス・二マスとズラしていきます。
さっきの”例3”と”例4”をアレンジしていきます。
例3・その2

例4・その2

どちらも縦の列ごとに2マスずつ上下をズラしました。
パッと見では大した変化はありませんが、たくさん描いて遠くから眺めてみるとけっこう印象が変わりますよ!

サイズを変える × 重ねる × 向きを変える
別の3つの組み合わせ方法もやってみましょう。
最初の”例2”の模様に『向きを変える』アレンジを加えます。
小さい菱形を一個飛ばしで向きを変え、正方形にします。
例2・その2

線だけではよくわからない場合、色をつけた模様を参考にしてみてください。
小さい図形の列の正方形と菱形が重なりあっていますよね。
この正方形が、 『向きを変える』アレンジを加えた部分ということです。
もとの菱形と正方形では若干大きさが異なりますが、グリッドの目盛りに沿って線を描くと自然と変わってしまうので、あまり気にしないでも大丈夫です。
サイズを変える × 重ねる × ズラす (移動) × 向きを変える
では最後に、4つのアレンジ全てを組み合わせた模様を描きます。
『例3・その2』と『例4・その2』をアレンジします。
この2つの模様はすでに3つアレンジを組み合わせているので、そこに最後のアレンジ『向きを変える』を加えてみます。
そしてついでにサイズにも変化をつけてみましょう。
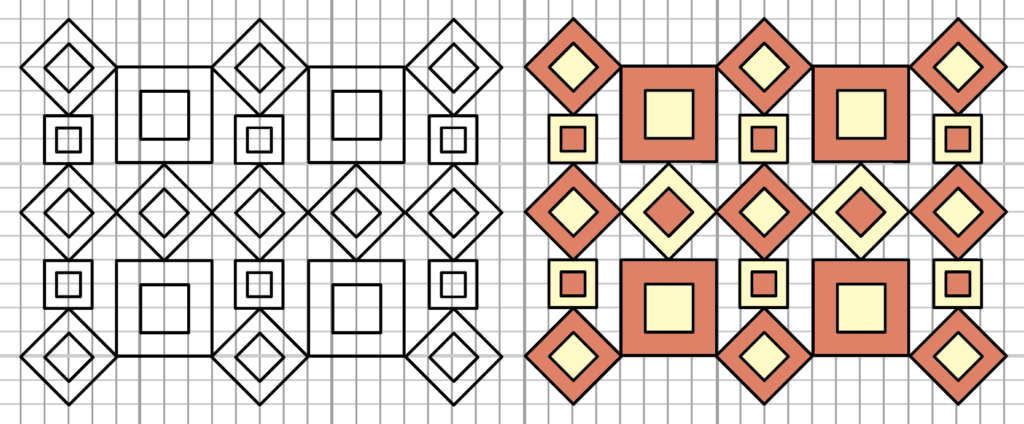

いかがでしょうか?
このような感じで、アレンジを組み合わせれば一つの図形だけでも様々な幾何学模様が描けるのです。
また今回はわかりやすく、規則性(法則性)のある模様を出しましたが、必ずしも規則性をガチッと組み込む必要はありません。
次の画像のようなランダムなアレンジでもいいと思います。
規則性(法則性)があることは模様の基本ではありますが、それが無いと模様じゃないのか?という点については、暇つぶしや趣味で描く分にはあまり重要ではありませんので!笑

1つの図形・形だけでも、配置の仕方次第で全く印象の違うものを作れる、ということをご理解いただければOKです。
それが、模様の奥深くて面白いところなのです。
例に出した幾何学模様以外にも、サイズや重ね方に色々な変化をつければたくさんの模様を作ることができますよ。

アレンジの組み合わせは何通り?
ところで気になった方もいるかもしれませんが、アレンジの組み合わせは何通りあるのか?ということです。
むやみやたらに組み合わせてみるより、先に組み合わせ方法を知っている方が模様を作りやすいのでは?という疑問もあるかと思います。
では実際、何通りの組み合わせがあるのかご説明いたします。
2つの組み合わせは6通り
まず、2つの組み合わせ方法です。
- ズラす (並行移動) × サイズを変える
- ズラす (並行移動) × 重ねる
- ズラす (並行移動) × 向きを変える
- サイズを変える × 重ねる
- サイズを変える × 向きを変える
- 向きを変える × 重ねる

3つの組み合わせは4通り
3つの組み合わせ方法はこちら。
- ズラす (並行移動) × サイズを変える × 重ねる
- ズラす (並行移動) × 向きを変える × 重ねる
- ズラす (並行移動) × サイズを変える × 向きを変える
- サイズを変える × 重ねる × 向きを変える

最後に4つ全てを組み合わせる
4つの組み合わせは、当然ですが1つだけです!
- ズラす (並行移動) × サイズを変える × 重ねる × 向きを変える

11通り × 3図形 = 33通りの模様パターン
ザッと組み合わせだけを羅列してみましたが、文面だけではそれぞれがどんな模様になるかイメージしにくいと思います。
ただとりあえず、組み合わせ方法は11通りもあるということです…!
これを例の図形「菱形」「三角形」「クの字図形」それぞれ1つずつ紹介するとしたら…
11通り × 3図形 = 33通りの模様パターン!
お、多い。。
全てを1つの記事でやりきるとしたら、多すぎる数の模様を紹介することになります…。
ちなみにですが、1つの方法に対しても複数バリエーションは考えられるので33通りをゆうに超えて50以上の模様パターンを出すことになりそうです…!
いくら何でも、1つの記事にしたら膨大な量になります。笑
ということで、それぞれの組み合わせ方法・やり方・描き方についてはこれから少しずつご紹介していこうと思います。
少しずつでも組み合わせ方法を覚えていけば、簡単な模様の描き方・特に幾何学模様というのは一気にバリエーションが豊かになり、それだけで楽しくなること間違いなしです。
1つの図形だけでも色んな幾何学模様が作れますので、ものすごく手頃な暇つぶしにもなると思います。
ご興味ありましたら、ぜひ引き続き当ブログをご覧くださいませ。















